2D/3D registration

Visualization of auto-differentiable registration with DiffDRR

To perform registration with DiffDRR, we do the following:

Obtain a target X-ray (this is the image whose pose parameters we wish to recovery)
Initialize a moving DRR module from a random camera pose
Measure the loss between the target X-ray and the moving DRR (we use normalized negative cross-correlation)
Backpropogate this loss to the pose parameters of the moving DRR and render from the new pose
Repeat Steps 3-4 until the loss has converged

1. Generate a target X-ray

Code

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import torch
from tqdm import tqdm

from diffdrr.data import load_example_ct
from diffdrr.drr import DRR
from diffdrr.metrics import NormalizedCrossCorrelation2d
from diffdrr.pose import convert
from diffdrr.registration import Registration
from diffdrr.visualization import plot_drr

# Make the ground truth X-ray
SDD = 1020.0
HEIGHT = 100
DELX = 4.0

subject = load_example_ct()
true_params = {
    "sdr": SDD,
    "alpha": 0.0,
    "beta": 0.0,
    "gamma": 0.0,
    "bx": 0.0,
    "by": 850.0,
    "bz": 0.0,
}
device = "cuda" if torch.cuda.is_available() else "cpu"

drr = DRR(subject, sdd=SDD, height=HEIGHT, delx=DELX).to(device)
rotations = torch.tensor(
    [[true_params["alpha"], true_params["beta"], true_params["gamma"]]]
)
translations = torch.tensor([[true_params["bx"], true_params["by"], true_params["bz"]]])
gt_pose = convert(
    rotations, translations, parameterization="euler_angles", convention="ZXY"
).to(device)
ground_truth = drr(gt_pose)

plot_drr(ground_truth)
plt.show()

2. Initialize a moving DRR from a random pose

The random pose is parameterized as a perturbation of the true pose. Angular perturbations are uniformly sampled from [-π/4, π/4] and translational perturbations are uniformly sampled from [-30, 30].

Code

# Make a random DRR
np.random.seed(1)


def pose_from_carm(sid, tx, ty, alpha, beta, gamma):
    rot = torch.tensor([[alpha, beta, gamma]])
    xyz = torch.tensor([[tx, sid, ty]])
    return convert(rot, xyz, parameterization="euler_angles", convention="ZXY")


def get_initial_parameters(true_params):
    alpha = true_params["alpha"] + np.random.uniform(-np.pi / 4, np.pi / 4)
    beta = true_params["beta"] + np.random.uniform(-np.pi / 4, np.pi / 4)
    gamma = true_params["gamma"] + np.random.uniform(-np.pi / 4, np.pi / 4)
    bx = true_params["bx"] + np.random.uniform(-30.0, 30.0)
    by = true_params["by"] + np.random.uniform(-30.0, 30.0)
    bz = true_params["bz"] + np.random.uniform(-30.0, 30.0)
    pose = pose_from_carm(by, bx, bz, alpha, beta, gamma).cuda()
    rotations, translations = pose.convert("euler_angles", "ZXY")
    return rotations, translations, pose


rotations, translations, pose = get_initial_parameters(true_params)
drr = DRR(subject, sdd=SDD, height=HEIGHT, delx=DELX).to(device)
with torch.no_grad():
    est = drr(pose)
plot_drr(est)
plt.show()

rotations, translations

(tensor([[-0.1303,  0.3461, -0.7852]], device='cuda:0'),
 tensor([[-11.8600, 828.8053, -24.4597]], device='cuda:0'))

3. Measure the loss between the target X-ray and moving DRR

We start by measuring the initial loss between the two images.

criterion = NormalizedCrossCorrelation2d()
criterion(ground_truth, est).item()

0.3365682363510132

If the negative normalized cross-correlation is greater than 0.999, we say the target and moving DRR have converged.

4. Backpropogate the loss to the moving DRR parameters

We also use this example to show how different optimizers affect the outcome of registration. The parameters we tweak are

lr_rotations: learning rate for rotation parameters
lr_translations: learning rate for translation parameters
momentum: momentum for stochastic gradient descent
dampening: dampening for stochastic gradient descent

A basic implementation of an optimization loop is provided below:

def optimize(
    reg: Registration,
    ground_truth,
    lr_rotations=5e-2,
    lr_translations=1e2,
    momentum=0,
    dampening=0,
    n_itrs=500,
    optimizer="sgd",  # 'sgd' or `adam`
):
    # Initialize an optimizer with different learning rates
    # for rotations and translations since they have different scales
    if optimizer == "sgd":
        optim = torch.optim.SGD(
            [
                {"params": [reg._rotation], "lr": lr_rotations},
                {"params": [reg._translation], "lr": lr_translations},
            ],
            momentum=momentum,
            dampening=dampening,
            maximize=True,
        )
        optimizer = optimizer.upper()
    elif optimizer == "adam":
        optim = torch.optim.Adam(
            [
                {"params": [reg._rotation], "lr": lr_rotations},
                {"params": [reg._translation], "lr": lr_translations},
            ],
            maximize=True,
        )
        optimizer = optimizer.title()
    else:
        raise ValueError(f"Unrecognized optimizer {optimizer}")

    params = []
    losses = [criterion(ground_truth, reg()).item()]
    for itr in (pbar := tqdm(range(n_itrs), ncols=100)):
        # Save the current set of parameters
        alpha, beta, gamma = reg.rotation.squeeze().tolist()
        bx, by, bz = reg.translation.squeeze().tolist()
        params.append([i for i in [alpha, beta, gamma, bx, by, bz]])

        # Run the optimization loop
        optim.zero_grad()
        estimate = reg()
        loss = criterion(ground_truth, estimate)
        loss.backward()
        optim.step()
        losses.append(loss.item())
        pbar.set_description(f"NCC = {loss.item():06f}")

        # Stop the optimization if the estimated and ground truth images are 99.9% correlated
        if loss > 0.999:
            if momentum != 0:
                optimizer += " + momentum"
            if dampening != 0:
                optimizer += " + dampening"
            tqdm.write(f"{optimizer} converged in {itr + 1} iterations")
            break

    # Save the final estimated pose
    alpha, beta, gamma = reg.rotation.squeeze().tolist()
    bx, by, bz = reg.translation.squeeze().tolist()
    params.append([i for i in [alpha, beta, gamma, bx, by, bz]])

    df = pd.DataFrame(params, columns=["alpha", "beta", "gamma", "bx", "by", "bz"])
    df["loss"] = losses
    return df

The PyTorch implementation of L-BFGS has a different API to many other optimizers in the library. Notably, it requires a closure function to evaluate the model multiple times before taking a step. Also, it does not accept per-parameter learning rates nor a maximize flag. Below is an implementation of L-BFGS for DiffDRR.

Code

def optimize_lbfgs(
    reg: Registration,
    ground_truth,
    lr,
    line_search_fn=None,
    n_itrs=500,
):
    # Initialize the optimizer and define the closure function
    optim = torch.optim.LBFGS(reg.parameters(), lr, line_search_fn=line_search_fn)

    def closure():
        if torch.is_grad_enabled():
            optim.zero_grad()
        estimate = reg()
        loss = -criterion(ground_truth, estimate)
        if loss.requires_grad:
            loss.backward()
        return loss

    params = []
    losses = [closure().abs().item()]
    for itr in (pbar := tqdm(range(n_itrs), ncols=100)):
        # Save the current set of parameters
        alpha, beta, gamma = reg.rotation.squeeze().tolist()
        bx, by, bz = reg.translation.squeeze().tolist()
        params.append([i for i in [alpha, beta, gamma, bx, by, bz]])

        # Run the optimization loop
        optim.step(closure)
        with torch.no_grad():
            loss = closure().abs().item()
            losses.append(loss)
            pbar.set_description(f"NCC = {loss:06f}")

        # Stop the optimization if the estimated and ground truth images are 99.9% correlated
        if loss > 0.999:
            if line_search_fn is not None:
                method = f"L-BFGS + strong Wolfe conditions"
            else:
                method = "L-BFGS"
            tqdm.write(f"{method} converged in {itr + 1} iterations")
            break

    # Save the final estimated pose
    alpha, beta, gamma = reg.rotation.squeeze().tolist()
    bx, by, bz = reg.translation.squeeze().tolist()
    params.append([i for i in [alpha, beta, gamma, bx, by, bz]])

    df = pd.DataFrame(params, columns=["alpha", "beta", "gamma", "bx", "by", "bz"])
    df["loss"] = losses
    return df

5. Run the optimization algorithm

Below, we compare the following gradient-based iterative optimization methods:

SGD
SGD + momentum
SGD + momentum + dampening
Adam
L-BFGS
L-BFGS + line search

Tip

For 2D/3D registration with Siddon’s method, we don’t need gradients calculated through the grid_sample (which uses nearest neighbors and therefore has gradients of zero w.r.t. the grid points). To avoid computing these gradients, which improves rendering speed, you can set stop_gradients_through_grid_sample=True.

# Keyword arguments for diffdrr.drr.DRR
kwargs = {
    "subject": subject,
    "sdd": SDD,
    "height": HEIGHT,
    "delx": DELX,
    "stop_gradients_through_grid_sample": True,  # Enables faster optimization
}

Code

# Base SGD
drr = DRR(**kwargs).to(device)
reg = Registration(
    drr,
    rotations.clone(),
    translations.clone(),
    parameterization="euler_angles",
    convention="ZXY",
)
params_base = optimize(reg, ground_truth)
del drr

# SGD + momentum
drr = DRR(**kwargs).to(device)
reg = Registration(
    drr,
    rotations.clone(),
    translations.clone(),
    parameterization="euler_angles",
    convention="ZXY",
)
params_momentum = optimize(reg, ground_truth, momentum=5e-1)
del drr

# SGD + momentum + dampening
drr = DRR(**kwargs).to(device)
reg = Registration(
    drr,
    rotations.clone(),
    translations.clone(),
    parameterization="euler_angles",
    convention="ZXY",
)
params_momentum_dampen = optimize(reg, ground_truth, momentum=5e-1, dampening=1e-4)
del drr

# Adam
drr = DRR(**kwargs).to(device)
reg = Registration(
    drr,
    rotations.clone(),
    translations.clone(),
    parameterization="euler_angles",
    convention="ZXY",
)
params_adam = optimize(reg, ground_truth, 1e-1, 5e0, optimizer="adam")
del drr

# L-BFGS
drr = DRR(**kwargs).to(device)
reg = Registration(
    drr,
    rotations.clone(),
    translations.clone(),
    parameterization="euler_angles",
    convention="ZXY",
)
params_lbfgs = optimize_lbfgs(reg, ground_truth, lr=3e-1)
del drr

# L-BFGS + line search
drr = DRR(**kwargs).to(device)
reg = Registration(
    drr,
    rotations.clone(),
    translations.clone(),
    parameterization="euler_angles",
    convention="ZXY",
)
params_lbfgs_wolfe = optimize_lbfgs(
    reg, ground_truth, lr=1e0, line_search_fn="strong_wolfe"
)
del drr

NCC = 0.999003:  52%|███████████████████████▍                     | 260/500 [00:07<00:06, 36.64it/s]

SGD converged in 261 iterations

NCC = 0.999026:  26%|███████████▉                                 | 132/500 [00:03<00:08, 41.12it/s]

SGD + momentum converged in 133 iterations

NCC = 0.999027:  26%|███████████▉                                 | 132/500 [00:03<00:09, 40.35it/s]

SGD + momentum + dampening converged in 133 iterations

NCC = 0.999022:  11%|████▉                                         | 53/500 [00:01<00:11, 39.29it/s]

Adam converged in 54 iterations

NCC = 0.999429:   7%|███▎                                          | 36/500 [00:14<03:11,  2.43it/s]

L-BFGS converged in 37 iterations

NCC = 0.999335:   2%|▉                                             | 10/500 [00:07<06:16,  1.30it/s]

L-BFGS + strong Wolfe conditions converged in 11 iterations

Code

parameters = {
    "SGD": (params_base, "#66c2a5"),
    "SGD + momentum": (params_momentum, "#fc8d62"),
    "SGD + momentum + dampening": (params_momentum_dampen, "#8da0cb"),
    "Adam": (params_adam, "#e78ac3"),
    "L-BFGS": (params_lbfgs, "#a6d854"),
    "L-BFGS + strong Wolfe conditions": (params_lbfgs_wolfe, "#ffd92f"),
}

with sns.axes_style("darkgrid"):
    plt.figure(figsize=(5, 3), dpi=200)
    for name, (df, color) in parameters.items():
        plt.plot(df["loss"], label=name, color=color)
    plt.xlabel("# Iterations")
    plt.ylabel("NCC")
    plt.legend()
    plt.show()

Visualizing the loss curves allows us to interpret interesting dynamics during optimization:

SGD and its variants all arrive at a local maximum around NCC = 0.95, and take differing numbers of iterations to escape the local maximum
While Adam arrives at the answer much faster, its loss curve is not monotonically increasing, which we will visualize in the next section
L-BFGS without line search is slow and each iteration takes much longer than first-order methods
L-BFGS with line seach is highly efficient in terms of number of iterations required, and it runs in roughly the same time as the best first-order gradient-based method

Visualize the parameter updates

Note that differences that between different optimization algorithms can be seen in the motion in the DRRs!

Code

from base64 import b64encode

from IPython.display import HTML, display

from diffdrr.visualization import animate

MAX_LENGTH = max(
    map(
        len,
        [
            params_base,
            params_momentum,
            params_momentum_dampen,
            params_adam,
            params_lbfgs,
            params_lbfgs_wolfe,
        ],
    )
)
drr = DRR(subject, sdd=SDD, height=HEIGHT, delx=DELX).to(device)


def animate_in_browser(df, skip=1, max_length=MAX_LENGTH, duration=30):
    if max_length is not None:
        n = max_length - len(df)
        df = pd.concat([df, df.iloc[[-1] * n]]).iloc[::skip]
    else:
        pass

    out = animate(
        "<bytes>",
        df,
        drr,
        ground_truth=ground_truth,
        verbose=True,
        device=device,
        extension=".webp",
        duration=duration,
        parameterization="euler_angles",
        convention="ZXY",
    )
    display(HTML(f"""<img src='{"data:img/gif;base64," + b64encode(out).decode()}'>"""))

animate_in_browser(params_base)

Precomputing DRRs: 100%|█████████████████| 262/262 [00:42<00:00,  6.10it/s]

animate_in_browser(params_momentum)

Precomputing DRRs: 100%|█████████████████| 262/262 [00:42<00:00,  6.10it/s]

animate_in_browser(params_momentum_dampen)

Precomputing DRRs: 100%|█████████████████| 262/262 [00:43<00:00,  6.03it/s]

animate_in_browser(params_adam)

Precomputing DRRs: 100%|█████████████████| 262/262 [00:43<00:00,  6.04it/s]

animate_in_browser(params_lbfgs)

Precomputing DRRs: 100%|█████████████████| 262/262 [00:43<00:00,  6.04it/s]

animate_in_browser(params_lbfgs_wolfe)

Precomputing DRRs: 100%|█████████████████| 262/262 [00:43<00:00,  6.06it/s]

L-BFGS with converges in so few iterations that a GIF with ~30 FPS is imperceptible. Here’s the same GIFs, but at 4 FPS.

animate_in_browser(params_lbfgs, max_length=len(params_lbfgs), duration=250)

Precomputing DRRs: 100%|███████████████████| 38/38 [00:06<00:00,  6.07it/s]

animate_in_browser(params_lbfgs_wolfe, max_length=len(params_lbfgs), duration=250)

Precomputing DRRs: 100%|███████████████████| 38/38 [00:07<00:00,  5.07it/s]

Visualize the optimization trajectories

Finally, using PyVista, we can visualize the trajectory of the estimated camera poses over time for each of the optimization methods.

SGD and its variants take more direct routes to the true camera pose (seagreen, orange, blue)
Adam takes the most winding route but gets there faster than SGD (pink)
Basic L-BFGS also takes a winding route, doubling back on itself at some points, and slowly reaches the solution (green)
L-BFGS with a line search function reaches the solution very directly, while incurring a higher runtime per iteration (yellow)

Code

import pyvista

from diffdrr.visualization import drr_to_mesh, img_to_mesh

pyvista.start_xvfb()


def df_to_mesh(drr, df):
    pts = []
    for idx in tqdm(range(len(df))):
        rot = torch.tensor(df.iloc[idx][["alpha", "beta", "gamma"]].tolist())
        xyz = torch.tensor(df.iloc[idx][["bx", "by", "bz"]].tolist())
        pose = convert(
            rot.unsqueeze(0),
            xyz.unsqueeze(0),
            parameterization="euler_angles",
            convention="ZXY",
        ).cuda()
        with torch.no_grad():
            source, _ = drr.detector(pose, None)
        pts.append(source.squeeze().cpu().tolist())
    return *img_to_mesh(drr, pose), lines_from_points(np.array(pts))


def lines_from_points(points):
    """Given an array of points, make a line set"""
    poly = pyvista.PolyData()
    poly.points = points
    cells = np.full((len(points) - 1, 3), 2, dtype=np.int_)
    cells[:, 1] = np.arange(0, len(points) - 1, dtype=np.int_)
    cells[:, 2] = np.arange(1, len(points), dtype=np.int_)
    poly.lines = cells
    return poly.tube(radius=3)


plotter = pyvista.Plotter()
ct = drr_to_mesh(drr.subject, "surface_nets", 150, verbose=False)
plotter.add_mesh(ct)

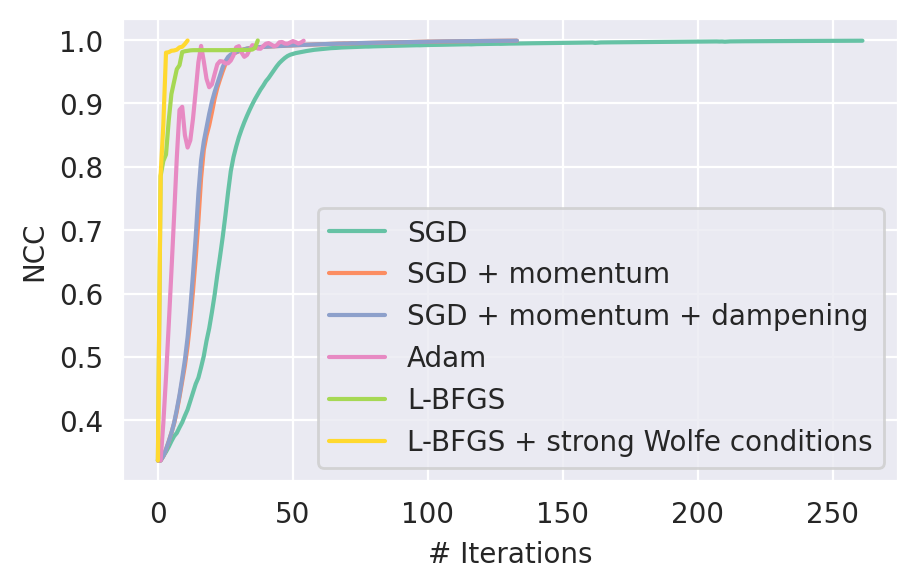
# SGD
camera, detector, texture, principal_ray, points = df_to_mesh(drr, params_base)
plotter.add_mesh(camera, show_edges=True, line_width=1.5)
plotter.add_mesh(principal_ray, color="#66c2a5", line_width=3)
plotter.add_mesh(detector, texture=texture)
plotter.add_mesh(points, color="#66c2a5")

# SGD + momentum
camera, detector, texture, principal_ray, points = df_to_mesh(drr, params_momentum)
plotter.add_mesh(camera, show_edges=True, line_width=1.5)
plotter.add_mesh(principal_ray, color="#fc8d62", line_width=3)
plotter.add_mesh(detector, texture=texture)
plotter.add_mesh(points, color="#fc8d62")

# SGD + momentum + dampening
camera, detector, texture, principal_ray, points = df_to_mesh(
    drr, params_momentum_dampen
)
plotter.add_mesh(camera, show_edges=True, line_width=1.5)
plotter.add_mesh(principal_ray, color="#8da0cb", line_width=3)
plotter.add_mesh(detector, texture=texture)
plotter.add_mesh(points, color="#8da0cb")

# Adam
camera, detector, texture, principal_ray, points = df_to_mesh(drr, params_adam)
plotter.add_mesh(camera, show_edges=True, line_width=1.5)
plotter.add_mesh(principal_ray, color="#e78ac3", line_width=3)
plotter.add_mesh(detector, texture=texture)
plotter.add_mesh(points, color="#e78ac3")

# L-BFGS
camera, detector, texture, principal_ray, points = df_to_mesh(drr, params_lbfgs)
plotter.add_mesh(camera, show_edges=True, line_width=1.5)
plotter.add_mesh(principal_ray, color="#a6d854", line_width=3)
plotter.add_mesh(detector, texture=texture)
plotter.add_mesh(points, color="#a6d854")

# L-BFGS + line search
camera, detector, texture, principal_ray, points = df_to_mesh(drr, params_lbfgs_wolfe)
plotter.add_mesh(camera, show_edges=True, line_width=1.5)
plotter.add_mesh(principal_ray, color="#ffd92f", line_width=3)
plotter.add_mesh(detector, texture=texture)
plotter.add_mesh(points, color="#ffd92f")

# Ground truth
camera, detector, texture, principal_ray = img_to_mesh(drr, gt_pose)
plotter.add_mesh(camera, show_edges=True, line_width=1.5)
plotter.add_mesh(principal_ray, color="black", line_width=3)
plotter.add_mesh(detector, texture=texture)

# Render the plot
plotter.add_axes()
plotter.add_bounding_box()

plotter.export_html("registration_runs.html")

100%|██████████████████████████████████████████████████████████████████████████████| 262/262 [00:00<00:00, 615.04it/s]
100%|██████████████████████████████████████████████████████████████████████████████| 134/134 [00:00<00:00, 641.46it/s]
100%|██████████████████████████████████████████████████████████████████████████████| 134/134 [00:00<00:00, 644.99it/s]
100%|████████████████████████████████████████████████████████████████████████████████| 55/55 [00:00<00:00, 647.42it/s]
100%|████████████████████████████████████████████████████████████████████████████████| 38/38 [00:00<00:00, 653.30it/s]
100%|████████████████████████████████████████████████████████████████████████████████| 12/12 [00:00<00:00, 626.87it/s]

from IPython.display import IFrame

IFrame("registration_runs.html", height=500, width=749)